\(\Large \require{AMScd} \begin{CD} B @>>k_A> A \\
@VVk_CV\\C \end{CD} \)
平均は,
\(\Large <t> = \displaystyle \int_{ 0 }^{ \infty } t_1 \cdot P(t_1) \cdot dt_1 =\displaystyle \int_{ 0 }^{ \infty } t_1 \cdot (k_A + k_C) \cdot exp \left[ -(k_A + k_C) \cdot t_1 \right] dt_1 \)
となります.
部分積分の公式より,
\(\Large (f \cdot g)' = f' \cdot g + f \cdot g' \)
\(\Large f' \cdot g = (f \cdot g)' - f \cdot g' \)
\(\Large \int f' \cdot g = (f \cdot g) - \int f \cdot g' \)
となります.ここで,
\(\Large f'=exp \left[ -(k_A + k_C) \cdot t_1 \right], \quad g = t_1 \)
\(\Large f=-\frac{1}{k_A + k_C} exp \left[ -(k_A + k_C) \cdot t_1 \right], \quad g' = t_1 \)
とおけば,
\(\Large \begin{eqnarray} <t> &=& \displaystyle \int_{ 0 }^{ \infty } t_1 \cdot (k_A + k_C) \cdot exp \left[ -(k_A + k_C) \cdot t_1 \right] dt_1 \\
&=& (k_A + k_C) \cdot \left[ -\frac{1}{k_A + k_C} exp \left[ -(k_A + k_C) \cdot t_1 \right] \times t_1 \right]_0^ \infty
-(k_A + k_C)\displaystyle \int_{ 0 }^{ \infty} -\frac{1}{k_A + k_C} exp \left[ -(k_A + k_C) \cdot t_1 \right] dt_1\\
&=&
-\frac{k_A + k_C}{(k_A + k_C)^2} \left[ exp \left[ -(k_A + k_C) \cdot t_1 \right] \right] _0^{ \infty} \\
&=&
\frac{1}{k_A + k_C} \\
\end{eqnarray} \)
となり,反応にかかる時間は,それぞれの速度定数の和の逆数となります.
ここで,興味深い点は,
kA, kCが同等である
と言うことです.つまり,
B,Cへのどちらの反応も平均反応時間は同じ
となります.もちろん,最終的な割合は異なりますが(計算はこちら).
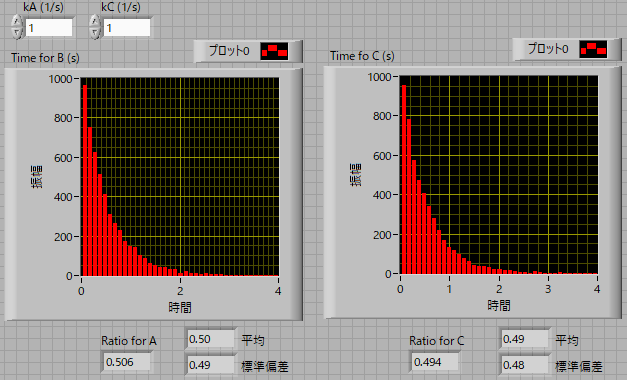
実際のモンテカルロシュミレーションでは,

となり,
\(\Large <t> = \frac{1}{k_A + k_C} \)
となります(1/(1+1)=0.5).速度定数を変えると,
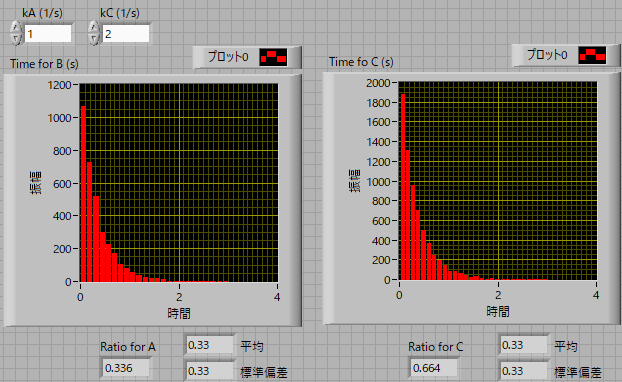
となり,A,Cどちらの反応にかかる時間も,
\(\Large <t> = \frac{1}{k_A + k_C} \)
となります(1/(1+2)=0.33).
次ページに,平衡・逐次反応について考えていきましょう.